
, where d is your distance from the light source. See Technical Requirements in the Orientation for a list of compatible browsers. Thus, the equation for the apparent brightness of a light source is given by the luminosity divided by the surface area of a sphere with radius equal to your distance from the light source, orį = L / 4 π d 2 This equation is not rendering properly due to an incompatible browser. So, a light source will appear four times fainter if you are twice as far away from it as someone else, and it will appear nine times fainter if you are three times as far away from it as someone else. The light has to spread out to cover 9 times as much area for a shell three times as large in radius. Since the same total amount of light is illuminating each spherical shell, the light has to spread out to cover 4 times as much area for a shell twice as large in radius. If you triple the radius, the surface area of the larger sphere increases by a factor of 9 = ( 3 2 ) This equation is not rendering properly due to an incompatible browser.

, then the surface area of the larger sphere is larger by a factor of 4 = ( 2 2 ) This equation is not rendering properly due to an incompatible browser. How bright will the same light source appear to observers fixed to a spherical shell with a radius twice as large as the first shell? Since the radius of the first sphere is d, and the radius of the second sphere would be 2 x d This equation is not rendering properly due to an incompatible browser.

The amount of dilution is related to the surface area of the spheres, which is given by:Ī = 4 π d 2 This equation is not rendering properly due to an incompatible browser. Each shell should receive the same total amount of energy per second from the star, but since each successive sphere is larger, the light hitting an individual section of a more distant sphere will be diluted compared to the amount of light hitting an individual section of a nearby sphere. In the above image, the entire spherical shell isn't illustrated, just a small section. As that energy gets emitted, you can picture it passing through spherical shells centered on the star. This idea is illustrated in this figure:Īgain, think of the luminosity-the energy emitted per second by the star-as an intrinsic property of the star. Why do light sources appear fainter as a function of distance? The reason is that as light travels towards you, it is spreading out and covering a larger area. There is a mathematical relationship that relates these three quantities–apparent brightness, luminosity, and distance for all light sources, including stars. An intrinsically faint, nearby star can appear to be just as bright to us on Earth as an intrinsically luminous, distant star. The variation in their brightness is caused by both variations in their luminosity and variations in their distance. Stars have a wide range of apparent brightness measured here on Earth. If you put an automobile headlight 10 feet away and a flashlight 10 feet away, the flashlight will appear fainter because its luminosity is smaller. However, not all light bulbs are the same luminosity. To think of this another way, given two light sources with the same luminosity, the closer light source will appear brighter. However, when the car passes you within 10 feet, its lights may appear blindingly bright. When the car is far away, even if its high beams are on, the lights will not appear too bright. So, everyone will measure a different apparent brightness for the same star if they are all different distances away from that star.įor an analogy with which you are familiar, consider again the headlights of a car. However, apparent brightness is not an intrinsic property of the star it depends on your location. Another way to look at these quantities is that the luminosity is an intrinsic property of the star, which means that everyone who has some means of measuring the luminosity of a star should find the same value.
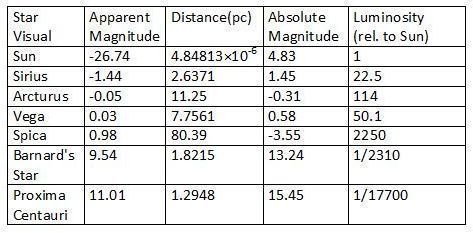
The difference between luminosity and apparent brightness depends on distance. The luminosity of a star, on the other hand, is the amount of light it emits from its surface. When I say apparent brightness, I mean how bright the star appears to a detector here on Earth. I am purposely being careful about my choice of words. Perhaps the easiest measurement to make of a star is its apparent brightness.


 0 kommentar(er)
0 kommentar(er)
